عدد غراهام

عدد غراهام Grahm number    (واللفظ الصحيح هو عدد غرام)  نسبة لعالم الرياضيات رون غراهام

وعدد غراهام هو أكبر عدد تم استخدامه يوما لإثبات مبرهنة رياضية

ولكن قبل ان نخوض في عدد غراهامعلينا اولا معرفة طريقة كتابة الاعداد الكبيرة وهذا ليس صعبا كما سترى،

كيف تكتب الاعداد الكبيرة

يمكنك أن تكتب المليون هكذا 1000000 وللاختصار يمكن كتابته على شكل 10⁶ يساوي 10 ×10 ×10×10 ×10 ×10

(عشرة مضروبة بنفسها 6 مرات وليس 6×10)

مليون	1000000	106
مليار	1000000000	109
جوجل	واحد وعلى يمينه 100 صفر	10100

طبعا العدد الذي في الاس يمكن أن يكون عددا كبيرا أيضا ،10¹⁰⁶هذا يساوي واحد وعلى يمينه مليون من الاصفار، ولن اقوم بكتابته بالطريقة التقليدية، وهنا يتضح لنا فائدة هذا الاسلوب في كتابة الارقام.

طريقة اخرى للكتابة هي باستخدام الاسهم

يمكنك أن تكتب 10³ على هذا الشكل 3↑10 ويمكنك أن تكتب المليون على هذا الشكل 10 السهم هنا ببساطة يشير للقوة أو الاس

لكن ماذا عن الاعداد الاكبر من هذا بكثير ، لو أردنا كتابة الرقم التالي

لاشك أن كتابته ستكون صعبة جدا ولاتنسى أيضا صعوبة اجراء العمليات الحسابية عليه

واحدة من الطرق ال مستخدة مايسمى

Tetration 

وتشبه الطريقة السابقة ولكن بالمزيد من الاسهم

 3  ↑↑10هذا يعني تكرار 10↑10 ثلاث مرات  ( 10↑10) ↑10

وبما أن 10↑10 تساوي 10¹⁰ اذا فان 3↑↑10 تساوي 10¹⁰¹⁰

لاحظ أن وجود السهمين بشير الى ان العدد الذي في اليسار سيتكرر على شكل "برج" ان جاز التعبير، وسيكون طول البرج نفس العدد الذي في اليمين، على هذا فإن

في الحقيقة من عند هذه النقطة تصبح الامور معقدة نوعا ما، لكن اذا استمريت في المتابعة أعدك أن الامر سيستحق العناء في النهاية، تخيل نفسك في مغامرة عقلية خلال الارقام

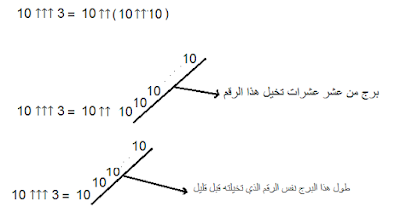
الان ماذا لو وضعنا ثلاثة أسهم؟ وهي طريقة صحيحة في الكتابة،  فلنقل 3↑↑↑10، بنفس المنطق السابق يمكننا كتابته هكذا    

   (10↑↑10) ↑↑10

 كما لاحظت يوجد نمط يتكرر ، كرر العدد الذي في اليسار بمقدار العدد الذي في اليمين.

نبدأ الان الانتقال الى عدد غراهام

في البداية عندنا g1

وهو رقم محدد بعينه وليس طريقة للكنابة

g1 = 3↑↑↑↑3  (رقم كبير جدا لاحظ الاسهم الاربعة)

بتطبيق ما تعلمناه سابفا

g1 = 3↑↑↑↑3 = 3↑↑↑3↑↑↑3) = 3 ↑ ↑ ↑ (3 ↑ ↑ (3 ↑↑3))

لأ أريد تحليل g1 أكثر من هذا ولكن قد وصلتك فكرة كم هو كبير الرقم g1

هناك أيضا g2 وهو رقم أضخم بكثير من g1

ببساطة نأخذ العدد الكبير جدا الذي هو g1   وليس عدد الاسهم ولكن g1 بحقيقته ، ويكون ذلك العدد هو عدد الاسهم في g2

نكرر هذه العملية مرة أخرى فنأخذ العدد الكبير الناتج من g2 ويكون عدد الاسهم في g3

وهكذا نعيد العملية نفسها لنحصل على g4 وg5 وg6 ....وحتى g64

وأخيرا وصلنا الى عدد غرام

g64 هو عدد غراهام وهو عدد كبير بلاشك يستحيل تخيله

الى هنا ينتهي الجزء الصعب ، بقي أن نعرف بماذا يستخدم عدد غراهام

انظر الى الشكل 1

يمثل مربع بأربعة أضلاع وخطين إضافـيـيـن قطريين لايصال كل زاوية بالاخرى فيكون المجموع ستة خطوط، المطلوب منا تلوين تلك الخطوط بلونبن فقط إما الاحمر أو الازرق، ولكن هناك شرط لصحة التلوين وهو أن لاتكون جميع الخطوط بنفس اللون وقد حققنا هذا الشرط فعلا في الشكل 1 وهو مربع داخل بعدين 2D، طول وعرض.

المكعب شكل ضمن ثلاثة ابعاد ،طول وعرض وارتفاع (شكل2)

ويمكننا رسمه بنفس الشروط السابقة ففي النهاية المكعب يتكون من ستة مربعات ، وكل ما علينا فعله هو ضمان أن لاتكون الوجوه العمودية أو الافقية ذات أضلاع متشابهة اللون، لاحظ أننا نتحدث عن الوجوه العمودية أو الافقية ولاتهمنا الوجوه الداخلية القطرية.

وماذا لو حاولنا رسم الشكل بطريقة رباعية الابعاد؟ هل يمكن رسمه بنفس الشروط؟ والجواب هو نعم ونستطيع أيضا رسمه ضمن تلك الشروط بخمسة ابعاد وستة ابعاد أيضا وتستمر السلسلة حتى تصل الى عدد غرام من الابعاد ففي حالة محاولتك لرسم الشكل الهندسي السابق بعدد غرام من الابعاد فانك لن تتمكن من تلوينه بنفس الشروط وستحصل بلاشك على واجهة ملونة جميع اضلاعها بنفس اللون ، وهذا هو استخدام عدد غراهام في الرياضيات

رائع بلاشك أليس كذلك؟ وقد استحق العناء

وبمكننا هنا ان نرى جمال الرياضيات وسحرها عدا اهميتها وتأثيرها المياشر وغير المباشر بالاخص الفيزياء وغيرها من العلوم الاخرى

---

ملحق 1

8/6/2016
المزيد من التوضيح لـ G1

مزيد من التوضيح لاستخدام رقم غراهام

Share on Facebook Share on Twitter Share on Google Plus